【学习笔记】week2-基础

发表于 | 更新于 | 分类于

写在之前
这次主要是基础，以及一些数学公式= =，参照《卷积神经网络的Python实现》以及李宏毅的视频~~

= 正文 =

批次（batch）

定义：批量更新的大小，直白的说就是每次训练是拿多少个样本进行训练。

当数据集较小时，可以采用 全数据集（Full Batch Learning） 的形式，这样训练的方向代表着样本总体的方向，使训练结果更加准确；并且Full Batch Learning可以使用弹性反向传播算法(RProp) 只基于梯度符号并且针对性单独更新因为不同权重的梯度值导致的权值。
当数据集较大时，以上的好处便不存在了；其一，随着数据集的海量增长和内存限制，一次性载入所有的数据进来变得越来越不可行。其二，以 Rprop 的方式迭代，会由于各个 Batch 之间的采样差异性，各次梯度修正值相互抵消，无法修正。这才有了后来均方根反向传播(RMSProp) 的妥协方案。

弹性反向传播(RProp)和均方根反向传播(RMSProp)都是一种权值更新算法，类似于SGD算法，其中，RMSProp是RProp算法的改良版。（自觉百度）

当Batch_Size==1时

当每次只训练一次样本时，即Batch_Size = 1。这就是在线学习（Online Learning） 。训练的结果难以达到收敛，其原因是Online Leaning训练的每一个样本都存在各自的特性性，不能代表其种类的特征性，导致在训练的时候朝着各自的方向修正，效果如图所示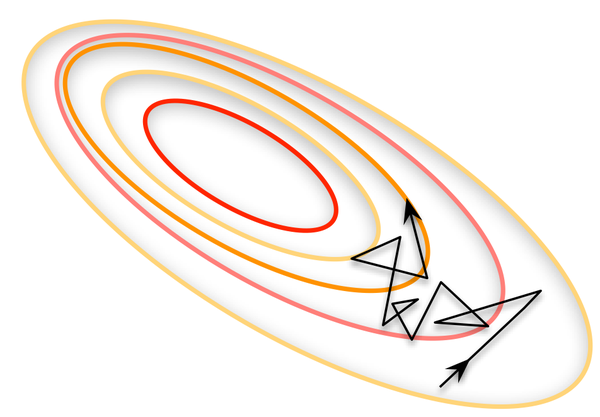
Batch_Size==1

当Batch_Size盲目增大，又不等于全部时

1.内存利用率提高了，但是内存容量可能撑不住了。
2.跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
3.Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。

当Batch_Size为合理大小时

1.内存利用率提高了，大矩阵乘法的并行化效率提高。
2.跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
3.在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小

以上总结：

这就是批梯度下降法（Mini-batches Learning）。因为如果数据集足够充分，那么用一半（甚至少得多）的数据训练算出来的梯度与用全部数据训练出来的梯度是几乎一样的。

损失函数

定义

损失函数（loss function，也叫代价函数，cost function）用来评价分值向量的好坏。分值向量与真实标签之间的差异越大，损失函数值就越大，反之则越小。
损失函数是深度学习的核心部分，通过它，可以将所要求的参数调整为需要的大小，其数学公式为: 

x1=x0-L_R*L_F(x0)
(其中x0，x1分别是调整前后的值，L_R为学习率，L_F为损失函数)

常用的损失函数

而目前我们常用的损失函数有
损失函数
代价函数
以上来自此博客（md的数学公式是真的烦，我之后在弄，顺便把图像也弄一下）

激活函数

定义

根据奥卡姆剃刀法则，神经网络采用的是最简单的线性模型 f(x) = wx+b, 并且线性模型的组合仍然为线性模型。但我们要解决的大部分问题又不仅仅是一个线性问题，因此在线性模型中增加非线性元素就显得尤其重要了。激活函数正是增加非线性的一个重要手段。

常用的激活函数

sigmoid函数

函数表达式为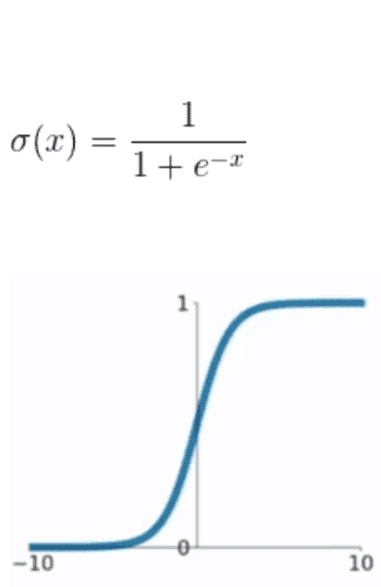

sigmoid是早期使用较多的激活函数，优点为

  1. 输出值为[0, 1], 符合概率分布
  2. x靠近0时斜率很大，对应为神经元兴奋区，远离0的区域斜率很小，对应为神经元抑制区

但其缺点也较为明显

  1. x稍微远离0, 导数就接近于0了，这样在反向传播优化w时，无论w取何值，梯度都很小，也就无法对w更新给出指导了，这种现象称为梯度弥散，在网络层级较深时尤其明显。
  2. 需要进行指数计算，比较耗时
  3. 容易造成梯度爆炸和梯度消失的结果
tanh

函数表达式为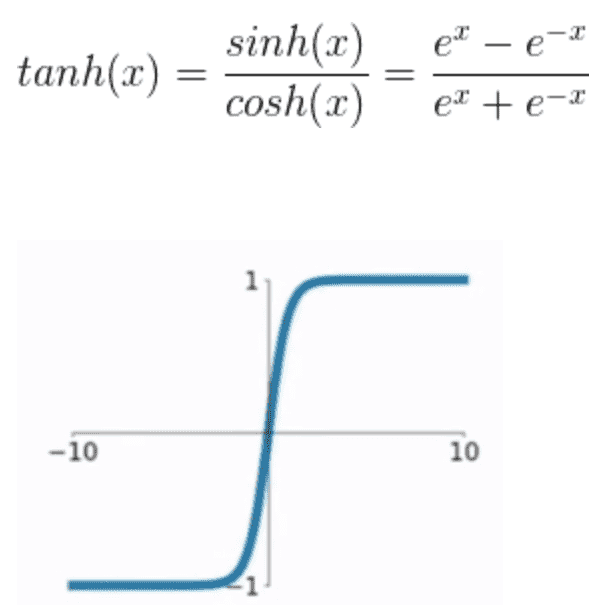

与sigmoid类似，只是Y值的分布是以0为中心，其问题也存在。

RELU

函数表达式为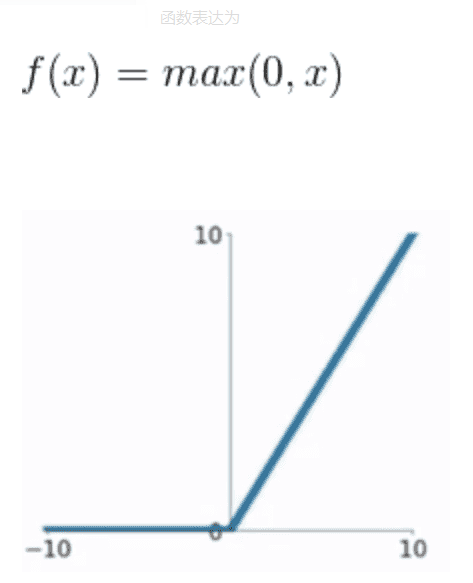

relu是当前使用最为频繁的激活函数，在几乎所有的CNN网络均使用relu作为激活函数，它解决了sigmoid和tanh的问题，优点为

  1. x大于0时，导数为1，在反向传播计算梯度时，不存在梯度弥散问题。
  2. x>0时，y=x, x<0时，y=0, 计算十分简单。

针对于relu的x<0部分，出现了一些变种函数，比如ELU和PRELU，均是针对x<0分支的改进，和relu大体相似。

学习率（Learning Rate）

学习率是指导我们该如何通过损失函数的梯度调整网络权重的超参数。学习率越低，损失函数的变化速度就越慢。虽然使用低学习率可以确保我们不会错过任何局部极小值，但也意味着我们将花费更长的时间来进行收敛，特别是在被困在高原区域的情况下。

下述公式表示了上面所说的这种关系。
new_weight = existing_weight — learning_rate * gradient

当学习率过小或者学习率过大都会对训练的情况造成很大的影响，如图：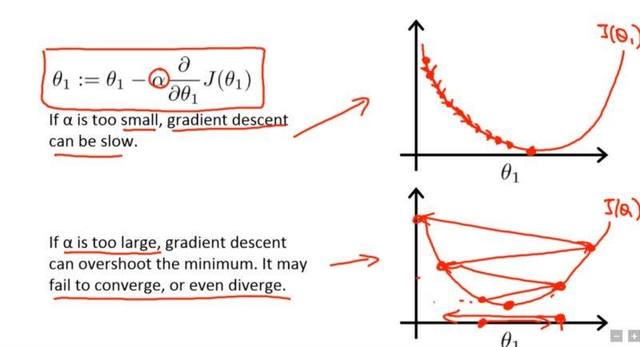

当学习率过小时，虽然能达到拟合，但需要的时间特别长；当学习率过大时，可能收敛不了，故学习率应适中。在实际操作情况下，一般学习率先大后小，先快速下降，后通过减小学习率达到收敛。
参考机器之心

学习率优化算法

学习率优化算法，在卷积神经网络一书中主要介绍了以下算法：

  • 随机梯度下降法
  • 动量法
  • AdaGrad
  • 。。。。

具体看书吧= =

反向传播

没啥好讲的，不是很了解= =
这里

0%